Polohované sklady - topologie skladu a algoritmus nejkratší vzdálenosti
Jak bylo zmíněno v předchozí kap. Polohované sklady - Zadávání pozic, pozice lze zadávat různým způsobem. Častým kritériem pro výběr pozic je jejich dostupnost, odvozená zejména od vzdálenosti pozice od místa, odkud resp. kam je třeba zboží přemístit. Ovšem dostupnost dané pozice s ohledem na vzdálenost se mění (záleží na tom, odkud a kam se zboží přemísťuje). Tudíž kromě ručně zadané dostupnosti jednotlivých pozic lze využít systému popisu topologie skladu a cest v něm, který dovolí automatický výpočet vzdáleností jednotlivých bodů ve skladu za pomocí tzv. algoritmu nejkratší cesty mezi dvěma body neboli Dijkstrova algoritmu.
Topologie se definuje pro každý sklad zvlášť. V rámci skladu můžeme uvažovat např. členění na budovy, v budovách na patra. V každém patře nechť je navržen systém tras spojujících jednotlivé uzly. Jako uzly jsou pak označeny jednotlivé křižovatky, odbočky a zlomy tras, případně další místa, ke kterým mají být přiřazeny pozice (viz dále). Trasy musí být ohodnoceny povinně vzdáleností a volitelně časovým údajem. Mohou existovat i trasy spojující patra (typicky výtah nebo dopravník). Některé uzly mohou být zároveň branami.
Každá pozice pak může mít přidělen jeden nebo více uzlů, ke kterým je nejbližší s udanou vzdáleností (a volitelně také časem) od těchto uzlů.
Při naskladnění nebo vyskladnění je výchozím údajem sklad – tím jsou dány možné brány. Výběrem brány je dána budova a patro a tím jsou dány dostupné uzly a trasy a tedy pozice, které se mají nabízet.
Dále objasníme metodu algoritmu nejkratší cesty mezi dvěma body neboli Dijkstrova algoritmu. Uvažujme pro lepší představu následující skladovou halu se dvěma branami (Gate A a B) a několika sestavami regálů:

Mezi regály jsou uličky (cesty), kterými se lze pohybovat. Vyznačíme čarami systém těchto uliček a zároveň vyznačíme body, kde se cesty kříží, rozbočují nebo lomí. Výsledek je na následujícím obrázku:

Nyní vyjmeme tento systém bodů a čar (křižovatek a cest), získáme síť uzlů a jejich spojnic (hran):

Abychom s nimi mohli dále pracovat, označíme jednotlivé uzly písmeny A – K a ke každé spojnici zapíšeme její délku (tzv. ohodnocení grafu):

Nyní chceme vyčíslit nejkratší možnou vzdálenost z brány Gate_A k ostatním uzlům. K tomu použijeme tzv. Dijkstrův algoritmus. Použijeme tabulku, do které pod sebe zapíšeme nejprve výchozí uzel (Gate_A) a pak seznam všech ostatních uzlů. Do sloupců budeme v jednotlivých krocích zapisovat tzv. dočasnou vzdálenost a za lomítkem označení posledního uzlu, ze kterého byla vzdálenost počítána (pochopíte za chvíli). Výchozí hodnoty v prvním sloupci budou u výchozího uzlu 0 a všech ostatních uzlů nekonečno (znamená, že vzdálenost ještě nebyla určena a v praxi se sem dosadí něco jako maxint). Následuje cyklus, ve kterém provádíme tyto kroky:
- Vybereme uzel s nejkratší dočasnou vzdáleností a tento uzel označíme (v naší tabulce žlutou barvou a silným okrajem). Znamená to, že tato vzdálenost je pro tento uzel konečná a definitivní (je to nejkratší vzdálenost z výchozího uzlu do tohoto uzlu). Je-li uzlů s nejmenší vzdáleností více stejných, vybereme libovolný jeden z nich (jedno který). Na začátku je to právě výchozí startovací uzel (Gate_A).
- Zjistíme všechny sousední uzly námi označeného uzlu, které mají zatím ještě dočasnou vzdálenost a pro ně spočteme novou dočasnou vzdálenost jako vzdálenost označeného uzlu plus vzdálenost tohoto uzlu od označeného. Pokud nově vypočtená vzdálenost je menší než aktuální vzdálenost tohoto uzlu, zapíšeme do následujícího sloupce nově vypočtenou vzdálenost a za lomítko poznačíme jméno našeho označeného uzlu. U všech ostatních uzlů, které mají zatím dočasnou vzdálenost, tuto opíšeme z předchozího sloupce.
- Cyklus opakujeme tak dlouho, až všechny uzly mají spočtenu definitivní vzdálenost (maximální počet kroků je roven počtu uzlů).
- Pokud síť není tzv. souvislá, tzn. že nejsou všechny body vzájemně propojeny (existuje tedy dva a více tzv. komponent souvislosti). To se v našem algoritmu pozná tak, že v některém kroku narazíme na uzel s nejmenší dočasnou vzdáleností rovnou nekonečnu.
Pro lepší pochopení popíšeme první kroky na konkrétních hodnotách v našem příkladu.
- 0.krok - Výchozí je sloupec 0., v něm označíme uzel Gate_A, vzdálenost pro něj zapíšeme 0 (vzdálenost sama od sebe). U ostatních uzlů zapíšeme aktuální dočasné vzdálenosti, které jsou zatím nekonečno (max).
- 1.krok - Dále budeme zapisovat do sloupce 1. Z něj vedou dvě cesty do vrcholu A a D. Uzel Gate_A má vzdálenost 0 (vzdálenost sama od sebe), vzdálenost uzlů Gate A a A (délka hrany Gate_A – A, což je 1), tedy vzdálenost z Gate_A do bodu A je celkem 1. Protože 1 je menší než prozatímní dočasná vzdálenost zapsaná pro uzel A (to je hodnota (max)), zapíšeme ji jako novou stanovenou dočasnou vzdálenost k uzlu A a to následovně: 1/Gate_A (za lomítko píšeme uzel, ze kterého jsme přišli, resp. uzel, který jsme naposledy označili). Podobně k uzlu D zapíšeme 1/Gate_A. U ostatních uzlů přepíšeme aktuální dočasné vzdálenosti, které jsou zatím stále nekonečno (max).
- 2.krok - Dále budeme zapisovat do sloupce 2. Ve sloupci 1 hledáme uzel s nejmenší vzdáleností – jsou dva, uzel A a D, vybereme první z nich, tedy uzel A a označíme ho (a dále už s ním nebudeme počítat). Z něj vedou cesty do uzlu B a D. Sečteme vzdálenost spočtenou v předchozím kroku pro označený uzel A (ta je 1) a vzdálenost uzlů A a B (délku hrany A – B, což je 6), celkem tedy 7. Protože 7 je menší než prozatímní dočasná vzdálenost zapsaná pro uzel B (to je hodnota (max)), zapíšeme ji jako novou stanovenou dočasnou vzdálenost k uzlu B. Tedy do sloupce 2 zapíšeme k uzlu B vzdálenost 7/A. Obdobně spočteme vzdálenost uzlu D od uzlu A označeného v předchozím kroku. Tj. sečteme vzdálenost spočtenou v předchozím kroku pro označený uzel A (ta je 1) a vzdálenost uzlů A a D (délku hrany A – D, což je 2), celkem tedy 3. Uzel D ale již má ve svých sloupcích zapsanou nižší dočasnou vzdálenost a to 1, nově spočtená tedy není menší, a proto u uzlu D ponecháme 1/Gate_A. U ostatních uzlů přepíšeme aktuální dočasné vzdálenosti, které jsou zatím stále nekonečno (max).
- Krok 3-12:
Pokračujeme dále, až jsou označeny všechny uzly. Čísla v označených políčkách udávají nejkratší možnou vzdálenost z Gate_A k danému uzlu. Cestu, jak se tam dá dostat, zrekonstruujeme odzadu z poznačených uzlů za lomítkem.
Výsledek viz následující tabulka:
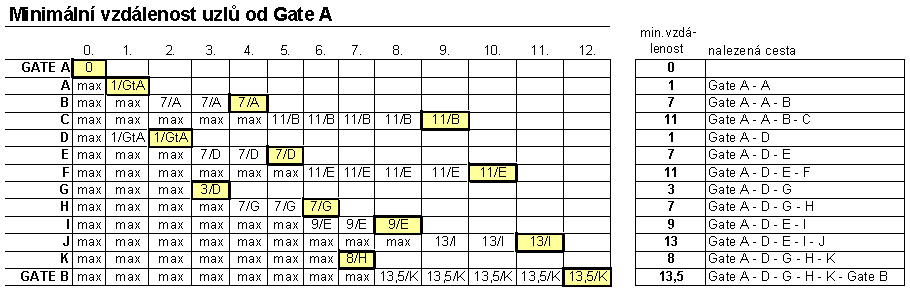
Podobně je možné zjistit vzdálenosti uzlů od Gate_B:
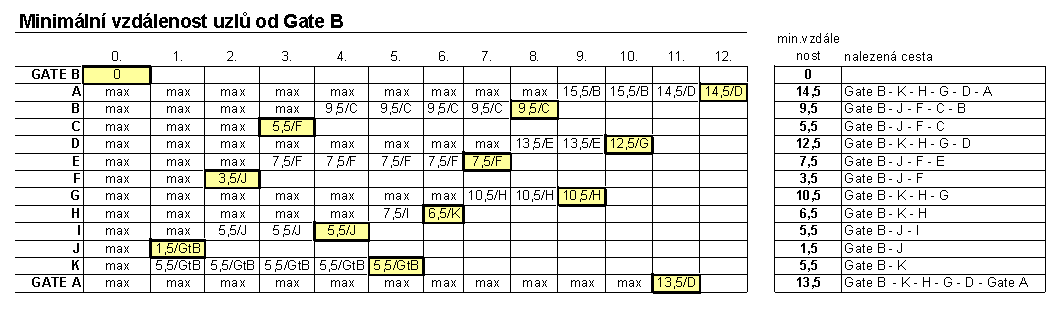
Algoritmus lze v praxi dále komplikovat:
- U cest mezi uzly (hran) lze např. kromě vzdálenosti sledovat ještě další vlastnost – např. čas potřebný k přesunu techniky po této dráze (může se lišit podle povrchu, terénu apod.). Tento údaj pak použijeme jako doplňkový v případě, že v některém kroku existuje více uzlů se stejnou nejmenší dočasnou vzdáleností. Pak z nich vybereme ten s menším časem.
- Můžeme také některé z cest označit jako obousměrné (jako výše), ale některé pouze jako jednosměrné. Na algoritmu to nic nemění, pouze v okamžiku, kdy zjišťujeme seznam sousedních uzlů, tak nebudeme počítat s těmi, kde sice spojnice je, ale vede "v protisměru". Jednosměrnost může být také stanovena jinak pro příjem zboží (naskladnění) a jinak pro výdej zboží (vyskladnění). Tím lze regulovat směr pohybu mechanizace.
Pomocí popsaného algoritmu lze tedy naprogramovat objekt, kterému předáme seznam uzlů, seznam jejich spojnic s udanou vzdáleností, případně časem a příznakem jednosměrnosti a označením, který z vrcholů je výchozí. Objekt potom vypočte nejmenší vzdálenosti od výchozího uzlu ke všem ostatním a dokáže sdělit schéma této cesty (přes které uzly cesta vede).
Výše popsaného algoritmu pro výpočet nejmenší vzdálenosti od výchozího uzlu ke všem ostatním se schématem této cesty (přes které uzly cesta vede) využijeme při výpočtech vzdáleností ve skladu a optimalizaci tras.
Systém popisu topologie skladu a výše popsaný algoritmus nejkratší cesty zatím není v systému implementován. Bude součástí některé z budoucích verzí.