Polohované sklady - topológia skladu a algoritmus najkratšej vzdialenosti
Ako bolo spomenuté v predchádzajúcej kap. Polohované sklady - Zadávanie pozícií, pozície je možné zadávať rôznym spôsobom. Častým kritériom výberu pozícií je ich dostupnosť, odvodená predovšetkým zo vzdialenosti pozície od miesta, odkiaľ resp. kam je potrebné tovar premiestniť. Dostupnosť danej pozície sa samozrejme s ohľadom na vzdialenosť mení (záleží na tom, odkiaľ a kam sa tovar premiestňuje). Tudíž kromě ručně zadané dostupnosti jednotlivých pozic lze využít systému popisu topologie skladu a cest v něm, který dovolí automatický výpočet vzdáleností jednotlivých bodů ve skladu za pomocí tzv. algoritmu nejkratší cesty mezi dvěma body neboli Dijkstrova algoritmu.
Topológia sa definuje pre každý sklad zvlášť. V rámci skladu můžeme uvažovat např. členění na budovy, v budovách na patra. V každém patře nechť je navržen systém tras spojujících jednotlivé uzly. Ako uzly sú potom označené jednotlivé križovatky, odbočky a zlomy trás, prípadne ďalšie miesta, ku ktorým majú byť priradené pozície (pozri ďalej). Trasy musia byť povinne ohodnotené vzdialenosťou a voliteľne časovým údajom. Môžu existovať i trasy spájajúce poschodia (typicky výťah alebo dopravník). Niektoré uzly môžu byť zároveň bránami.
Každá pozice pak může mít přidělen jeden nebo více uzlů, ke kterým je nejbližší s udanou vzdáleností (a volitelně také časem) od těchto uzlů.
Pri naskladnení alebo vyskladnení je východiskovým údajom sklad – tým sú dané možné brány. Výberom brány je daná budova a poschodie a sú tak dané dostupné uzly a trasy, teda pozície, ktoré sa majú ponúkať.
Ďalej objasníme metódu algoritmu najkratšej cesty medzi dvomi bodmi, teda Dijkstrovho algoritmu. Majme kvôli lepšej predstave nasledujúcu skladovú halu s dvomi bránami (Gate A a B) a niekoľkými zostavami regálov:
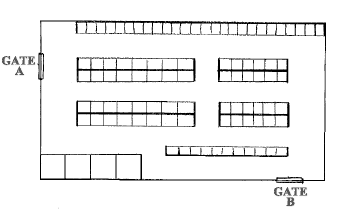
Medzi regálmi sú uličky (cesty), ktorými sa je možné pohybovať. Vyznačíme čiarami systém týchto uličiek a zároveň vyznačíme body, kde sa cesty križujú, rozbiehajú alebo lomia. Výsledok je na nasledujúcom obrázku:
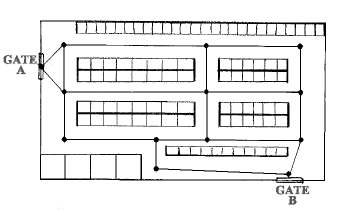
Teraz tento systém bodov a čiar (križovatiek a ciest) vyberieme, získame tak sieť uzlov a ich spojníc (hrán):
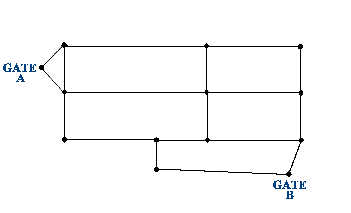
Abychom s nimi mohli dále pracovat, označíme jednotlivé uzly písmeny A – K a ke každé spojnici zapíšeme její délku (tzv. ohodnocení grafu):
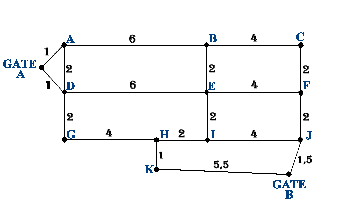
Nyní chceme vyčíslit nejkratší možnou vzdálenost z brány Gate_A k ostatním uzlům. K tomu použijeme tzv. Dijkstrův algoritmus. Použijeme tabuľku, do ktorej pod seba zapíšeme najskôr východiskový uzol (Gate_A) a potom zoznam všetkých ostatných uzlov. Do sloupců budeme v jednotlivých krocích zapisovat tzv. dočasnou vzdálenost a za lomítkem označení posledního uzlu, ze kterého byla vzdálenost počítána (pochopíte za chvíli). Výchozí hodnoty v prvním sloupci budou u výchozího uzlu 0 a všech ostatních uzlů nekonečno (znamená, že vzdálenost ještě nebyla určena a v praxi se sem dosadí něco jako maxint). Nasleduje cyklus, v ktorom vykonávame tieto kroky:
- Vybereme uzel s nejkratší dočasnou vzdáleností a tento uzel označíme (v naší tabulce žlutou barvou a silným okrajem). Znamená to, že tato vzdálenost je pro tento uzel konečná a definitivní (je to nejkratší vzdálenost z výchozího uzlu do tohoto uzlu). Je-li uzlů s nejmenší vzdáleností více stejných, vybereme libovolný jeden z nich (jedno který). Na začiatku je to práve východiskový štartovací uzol (Gate_A).
- Zistíme všetky susedné uzly nami označeného uzla, ktoré majú zatiaľ ešte dočasnú vzdialenosť a vypočítame pre ne novú dočasnú vzdialenosť ako vzdialenosť označeného uzla plus vzdialenosť tohto uzla od označeného. Pokiaľ je novo vypočítaná vzdialenosť menšia ako aktuálna vzdialenosť tohto uzla, zapíšeme do nasledujúceho stĺpca novo vypočítanú vzdialenosť a za lomku poznačíme meno nášho označeného uzla. U všech ostatních uzlů, které mají zatím dočasnou vzdálenost, tuto opíšeme z předchozího sloupce.
- Cyklus opakujeme tak dlho, kým nemajú všetky uzly spočítanú definitívnu vzdialenosť (maximálny počet krokov sa rovná počtu uzlov).
- Pokiaľ sieť nie je tzv. súvislá, tzn. že nie sú všetky body navzájom prepojené (existuje teda dva a viac tzv. komponentov súvislosti). To se v našem algoritmu pozná tak, že v některém kroku narazíme na uzel s nejmenší dočasnou vzdáleností rovnou nekonečnu.
Pro lepší pochopení popíšeme první kroky na konkrétních hodnotách v našem příkladu.
- 0.krok - Výchozí je sloupec 0., v něm označíme uzel Gate_A, vzdálenost pro něj zapíšeme 0 (vzdálenost sama od sebe). Pre ostatné uzly zapíšeme aktuálne dočasné vzdialenosti, ktoré sú zatiaľ nekonečno (max).
- 1.krok - Ďalej budeme zapisovať do stĺpca 1. Z něj vedou dvě cesty do vrcholu A a D. Uzol Gate_A má vzdialenosť 0 (vzdialenosť sama od seba), vzdialenosť uzlov Gate A a A (dĺžka hrany Gate_A – A, čo je 1), teda vzdialenosť z Gate_A do bodu A je celkom 1. Protože 1 je menší než prozatímní dočasná vzdálenost zapsaná pro uzel A (to je hodnota (max)), zapíšeme ji jako novou stanovenou dočasnou vzdálenost k uzlu A a to následovně: 1/Gate_A (za lomku píšeme uzol, z ktorého sme prišli, resp. uzol, ktorý sme naposledy označili). Podobně k uzlu D zapíšeme 1/Gate_A. Pre ostatné uzly prepíšeme aktuálne dočasné vzdialenosti, ktoré sú zatiaľ stále nekonečno (max).
- 2.krok - Ďalej budeme zapisovať do stĺpca 2. Ve sloupci 1 hledáme uzel s nejmenší vzdáleností – jsou dva, uzel A a D, vybereme první z nich, tedy uzel A a označíme ho (a dále už s ním nebudeme počítat). Z něj vedou cesty do uzlu B a D. Sčítame vzdialenosť spočítanú v predchádzajúcom kroku pre označený uzol A (tá je 1) a vzdialenosť uzlov A a B (dĺžku hrany A – B, čo je 6), celkom teda 7. Protože 7 je menší než prozatímní dočasná vzdálenost zapsaná pro uzel B (to je hodnota (max)), zapíšeme ji jako novou stanovenou dočasnou vzdálenost k uzlu B. Tedy do sloupce 2 zapíšeme k uzlu B vzdálenost 7/A. Rovnakým spôsobom vypočítame vzdialenosť uzla D od uzla A označeného v predchádzajúcom kroku. Tzn. sčítame vzdialenosť spočítanú v predchádzajúcom kroku pre označený uzol A (tá je 1) a vzdialenosť uzlov A a D (dĺžku hrany A – D, čo je 2), celkom teda 3. Uzol D ale už má vo svojich stĺpcoch zapísanú nižšiu dočasnú vzdialenosť, a to 1, novo spočítaná teda nie je menšia, a preto pri uzle D ponecháme 1/Gate_A. Pre ostatné uzly prepíšeme aktuálne dočasné vzdialenosti, ktoré sú zatiaľ stále nekonečno (max).
- Krok 3-12:
Pokračujeme ďalej, až kým sú označené všetky uzly. Čísla v označených políčkách udávají nejkratší možnou vzdálenost z Gate_A k danému uzlu. Cestu, jak se tam dá dostat, zrekonstruujeme odzadu z poznačených uzlů za lomítkem.
Výsledok viď nasledujúca tabuľka:
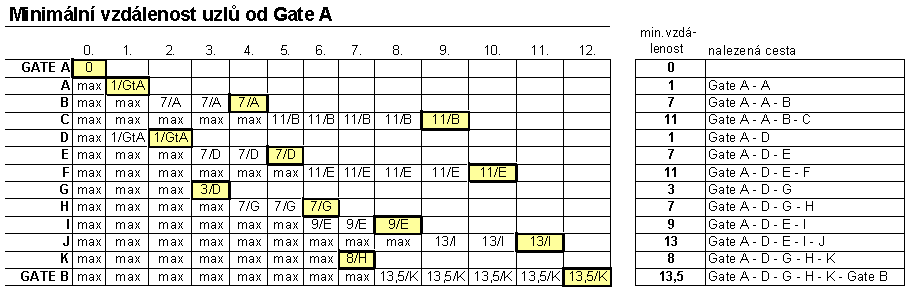
Podobne je možné zistiť vzdialenosti uzlov od Gate_B:
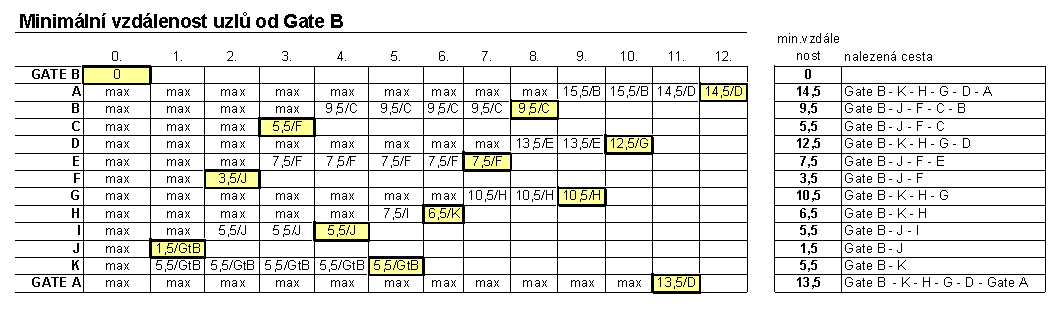
Algoritmus je možné v praxi ďalej komplikovať:
- U cest mezi uzly (hran) lze např. kromě vzdálenosti sledovat ještě další vlastnost – např. čas potřebný k přesunu techniky po této dráze (může se lišit podle povrchu, terénu apod.). Tento údaj pak použijeme jako doplňkový v případě, že v některém kroku existuje více uzlů se stejnou nejmenší dočasnou vzdáleností. Pak z nich vybereme ten s menším časem.
- Můžeme také některé z cest označit jako obousměrné (jako výše), ale některé pouze jako jednosměrné. Na algoritmu to nic nemění, pouze v okamžiku, kdy zjišťujeme seznam sousedních uzlů, tak nebudeme počítat s těmi, kde sice spojnice je, ale vede "v protisměru". Jednosmernosť môže byť tiež stanovená inak pre príjem tovaru (naskladnenie) a inak pre výdaj tovaru (vyskladnenie). Je tak možné regulovať smer pohybu mechanizácie.
Pomocí popsaného algoritmu lze tedy naprogramovat objekt, kterému předáme seznam uzlů, seznam jejich spojnic s udanou vzdáleností, případně časem a příznakem jednosměrnosti a označením, který z vrcholů je výchozí. Objekt potom vypočíta najmenšie vzdialenosti od východiskového uzla k všetkým ostatným a dokáže vyjadriť schému tejto cesty (cez ktoré uzly cesta vedie).
Vyššie popísaný algoritmus na výpočet najmenšej vzdialenosti od východiskového uzla k všetkým ostatným so schémou tejto cesty (cez ktoré uzly cesta vedie) využijeme pri výpočtoch vzdialeností v sklade a optimalizácii trás.
Systém popisu topológie skladu a vyššie popísaný algoritmus najkratšej cesty zatiaľ nie je v systéme implementovaný. Bude súčasťou niektorej z budúcich verzií.